| A Trigonometric Formula for the Surface area of a Triangle: | | The general formula for the area of a triangle is well known. While the formula shows the letters b and h, it is actually the pattern of the formula that is of import. The surface area of a triangle equals ½ the length of 1 side times the height drawn to that side (or an extension of that side).
| General Formula for Area of Triangle:
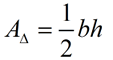
b = length of a side (base)
h = tiptop describe to that side | | The area of ΔABC tin exist expressed every bit: 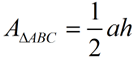
where a represents the side (base of operations)
and h represents the height fatigued to that side. | 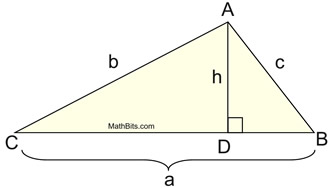 | Using trigonometry, allow's take another look at this diagram.
In the correct triangle CDA, we can state that:
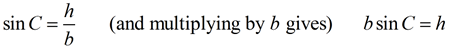
The height, h , of the triangle can be expressed as b sin C .
| Substituting this new expression for the height, h, into the full general formula for the area of a triangle gives:
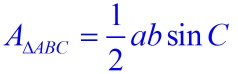
where a and b can be any two sides and
C is the included bending. | 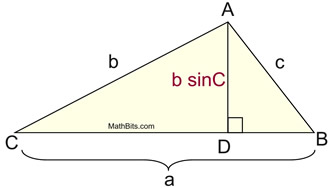 | |  | The area of a triangle tin can be expressed using the lengths of ii sides and the sine of the included angle. AreaΔ = ½ ab sin C. | | You may run into this referred to as the SAS formula for the area of a triangle. | With this new formula, we no longer have to rely on finding the distance (height) of a triangle in order to find its expanse. Now, if we know ii sides and the included bending of a triangle, we can detect the area of the triangle. This is a valuable new formula! 
 | Given the triangle at the right, find its area. Express the answer to the nearest hundredth of a square unit. | 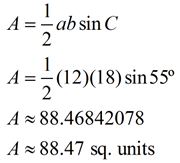 | When using your graphing figurer, exist sure you are in Degree mode, or using the caste symbol. | | 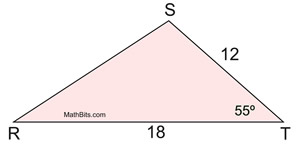
Let a = ST, b = RT, and C = ∠RTS. |
 Given the parallelogram shown at the right, discover its area to the nearest square unit. The diagonal of a parallelogram divides information technology into two congruent triangles. Then the total area of the parallelogram volition be TWICE the expanse of one of the triangles formed by the diagonal. This example shows that by doubling the triangle area formula, we have created a formula for finding the area of a parallelogram, given 2 next sides (a and b) and the included angle, C. 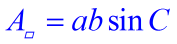
Area of Parallelogram
| 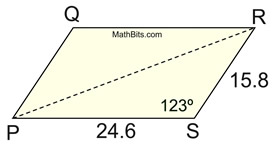
Let a = PS, b - RS, and C =∠PSR.
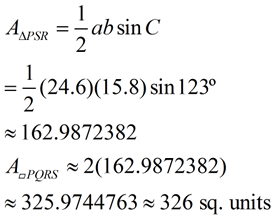
|
 Given the parallelogram shown at the correct, discover its Verbal surface area. If a question asks for an Verbal reply, do not use your calculator to find the sin 60º since it volition be a rounded value. To get an Verbal value for sin 60º, use the 30º-60º-90º special triangle which gives the sin 60º to exist 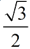 . .
Notice that we are using the formula for the area of a parallelogram we discovered in Example 2. | 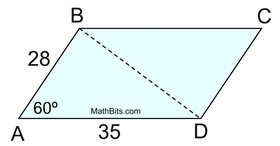
Let a = AD, b = AB, and C = ∠BAD.
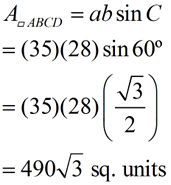
| |  | For help with
this formula on
your calculator,
click hither. | 
Deriving this formula:
NOTE: The Mutual Core Standard G.SRT.9 states "Derive the formula A = ½ab sin(C) for the surface area of a triangle by drawing an auxiliary line from a vertex perpendicular to the reverse side." This statement tin be interpreted equally applying only to acute triangles. This site will, however, examine both "acute" and "birdbrained" triangles in deriving the formula. Case 1: Astute Triangle If this formula truly works (and it does!), nosotros should be able to use the formula using any bending in the triangle. And so, when attempting to "derive" this formula, we should testify that it tin be "developed" using whatsoever (and every) angle in the triangle. In the case shown above, we developed the formula using acute ∠C. The same approach can be used to constitute the relationship using acute ∠B: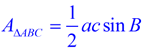 . When ∠A is a third acute bending, we can draw some other internal distance (summit) and apply this same arroyo a tertiary time, getting: . When ∠A is a third acute bending, we can draw some other internal distance (summit) and apply this same arroyo a tertiary time, getting: 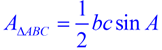 . .  Case two: Obtuse Triangle
Can we still develop this formula if ∠A is an obtuse angle? The respond is "yeah", only it volition require more work and some more trigonometric information. We volition have a brief await at what is involved when ∠A is an obtuse angle, only these concepts will be more fully developed in upcoming courses. Annotation: to maintain the use of a single alphabetic character to represent the angle in our formula, nosotros will be referring to ∠BAC in the diagram below, as ∠A. When ∠A is an obtuse angle, the altitude fatigued from C or B will exist outside of the triangle. Draw the altitude from C to the line containing the opposite side. ΔCAE is a right triangle, just unfortunately it does non comprise ∠A that we need for our formula. | 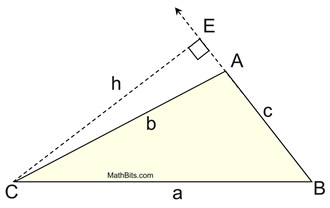 | | We know, however, that ∠CAE is supplementary to ∠A, since they form a linear pair.
We can state that m∠CAE = 180 - m∠A and from ΔCAE that 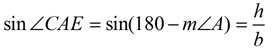 . .
If nosotros use a trigonometric fact that sin∠A = sin(180 - m∠A), nosotros tin can substitute and get:
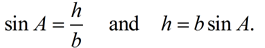 (Later on multiplying both sides of the starting time equation past b.) (Later on multiplying both sides of the starting time equation past b.)
Now, substitution into the full general formula for the area of a triangle will give us our desired formula: 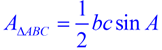 . . | | sin∠A = sin (180 - m∠A)
Recollect that the functions of sine, cosine, and tangent are defined only for acute angles in a right triangle.
So, how do nosotros discover the sine of an birdbrained angle? We cannot apply the sides of the triangle to find sin∠BAC considering the angle does not reside in a right triangle. We can, however, find sin∠BAD which deals with an astute angle in a right triangle. ∠BAD is the supplement of ∠BAC since they grade a linear pair. | 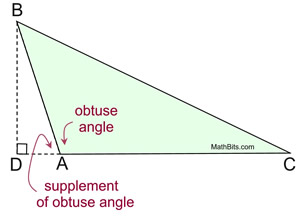 | | The sine of an obtuse angle is divers to exist the sine of the supplement of the angle.
Thus, sin∠A = sin (180 - chiliad∠A).
On your graphing reckoner, sin(50º) = 0.7660444431 and sin(130º) = 0.7660444431show this fact to be true. These angles are supplementary since 50º + 130º = 180º.
| | WHY does sin∠A = sin (180 - one thousand∠A)? This topic volition be explored in more than detail in upcoming courses.
To understand "why" this human relationship is true, we demand a coordinate grid. Right triangle DEF is drawn in quadrant I, as shown. If nosotros draw an bending of 130º, and drib a perpendicular to the x-axis from signal H where DH = DF, we will create a reflection of ΔDEF over the y-axis. This reflected triangle (ΔDGH) is congruent to ΔDEF and both triangles have the same lengths for their sides opposite the 50º. It should be noted that both opposite sides deal with positive y-values (designating direction above the x-axis).
| 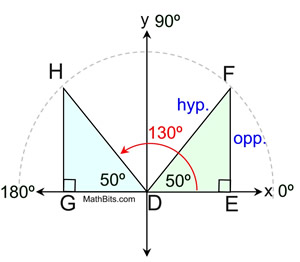
50º and 130º are supplementary.
| | When dealing with birdbrained angles (such as 130º), the corresponding acute bending (50º) is used to determine the sine, cosine or tangent of that birdbrained angle. This corresponding acute angle is called a "reference angle". | 
NOTE: The re-posting of materials (in part or whole) from this site to the Net is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |

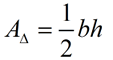
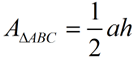

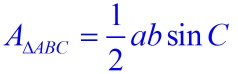

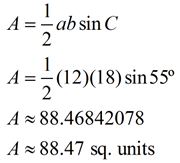


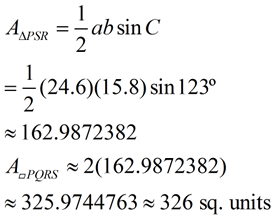

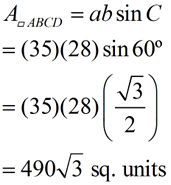

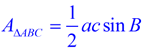 . When ∠A is a third acute bending, we can draw some other internal distance (summit) and apply this same arroyo a tertiary time, getting:
. When ∠A is a third acute bending, we can draw some other internal distance (summit) and apply this same arroyo a tertiary time, getting: 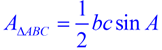 .
. 


0 Response to "How To Find Area Of Non Right Triangle"
Post a Comment